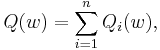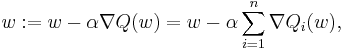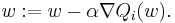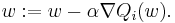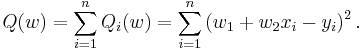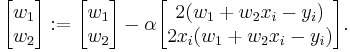Stochastic gradient descent

Stochastic gradient descent is an optimization method for minimizing an objective function that is written as a sum of differentiable functions.

Contents

Background

Main article: M-estimation
See also: Estimating equation

Both statistical estimation and machine learning consider the problem of minimizing an objective function that has the form of a sum:

Q(w) = \sum_{i=1}^n Q_i(w),

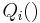where the parameter w is to be estimated and where typically each summand function Q_i( ) is associated with the i-th observation in the data set (used for training).

In classical statistics, sum-minimization problems arise in least squares and in maximum-likelihood estimation (for independent observations). The general class of estimators that arise as minimizers of sums are called M-estimators. However, in statistics, it has been long recognized that requiring even local minimization is too restrictive for some problems of maximum-likelihood estimation, as shown for example by Thomas Ferguson's example.[1] Therefore, contemporary statisticial theorists often consider stationary points of the likelihood function (or zeros of its derivative, the score function, and other estimating equations).

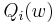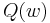The sum-minimization problem also arises for empirical risk minimization: In this case, Q_i(w) is the value of loss function at i-th example, and Q(w) is the empirical risk.

When used to minimize the above function, a standard (or "batch") gradient descent method would perform the following iterations :

w�:= w - \alpha \nabla Q(w) = w - \alpha \sum_{i=1}^n \nabla Q_i(w),

where \alpha is a step size (sometimes called the learning rate in machine learning).

In many cases, the summand functions have a simple form that enables inexpensive evaluations of the sum-function and the sum gradient. For example, in statistics, one-parameter exponential families allow economical function-evaluations and gradient-evaluations.

However, in other cases, evaluating the sum-gradient may require expensive evaluations of the gradients from all summand functions. When the training set is enormous and no simple formulas exist, evaluating the sums of gradients becomes very expensive, because evaluating the gradient requires evaluating all the summand functions' gradients. To economize on the computational cost at every iteration, stochastic gradient descent samples a subset of summand functions at every step.

Iterative method

In stochastic (or "on-line") gradient descent, the true gradient of 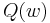Q(w) is approximated by a gradient at a single example:

w�:= w - \alpha \nabla Q_i(w).

As the algorithm sweeps through the training set, it performs the above update for each training example. Several passes over the training set are made until the algorithm converges. Typical implementations may also randomly shuffle training examples at each pass and use an adaptive learning rate.

In pseudocode, stochastic gradient descent with shuffling of training set at each pass can be presented as follows:

  • Choose an initial vector of parameters w and learning rate \alpha.
  • Repeat until an approximate minimum is obtained:
    • Randomly shuffle examples in the training set.
    • For 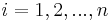\! i=1, 2, ..., n, do:
      • \! w�:= w - \alpha \nabla Q_i(w).

There is a compromise between the two forms, which is often called "mini-batches", where the true gradient is approximated by a sum over a small number of training examples.

The convergence of stochastic gradient descent has been analyzed using the theories of convex minimization and of stochastic approximation. Briefly, stochastic gradient methods need not converge to a global minimum unless the objective function is convex --- or more generally unless the problem has convex lower level sets and the function has the monotone property called "pseudoconvexity" in optimization theory, and finally the step-sizes are very small.[2]

Example

Let's suppose we want to fit a straight line 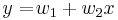y = \! w_1 %2B w_2 x to a training set of two-dimensional points \! (x_1, y_1), \ldots, (x_n, y_n) using least squares. The objective function to be minimized is:

Q(w) = \sum_{i=1}^n Q_i(w) = \sum_{i=1}^n \left(w_1 %2B w_2 x_i - y_i\right)^2.

The last line in the above pseudocode for this specific problem will become:

\begin{bmatrix} w_1 \\ w_2 \end{bmatrix}�:= \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} - \alpha \begin{bmatrix} 2(w_1 %2B w_2 x_i - y_i) \\ 2x_i(w_1 %2B w_2 x_i - y_i) \end{bmatrix}.

Applications

Some of the most popular stochastic gradient descent algorithms are the least mean squares (LMS) adaptive filter and the backpropagation algorithm.

References

  1. ^ Ferguson, Thomas S. (1982). "An inconsistent maximum likelihood estimate". J. Am. Stat. Assoc. 77 (380): 831–834. JSTOR 2287314. 
  2. ^ Kiwiel, Krzysztof C. (2001). "Convergence and efficiency of subgradient methods for quasiconvex minimization". Mathematical Programming (Series A) (Berlin, Heidelberg: Springer) 90 (1): pp. 1-25. doi:10.1007/PL00011414. ISSN 0025-5610. MR1819784. 

External links